فهم الشبكات العصبية

من العصبون إلى الشبكات العصبية المتكررة RNN والشبكات العصبية الالتفافية CNN والتعلُّم العميق Deep Learning

تعتبر الشبكات العصبية من أكثر خوارزميات التعلم الآلي شيوعًا في الوقت الحاضر فقد ثبت بمرور الوقت وبشكل حاسم أنها تتفوق على الخوارزميات الأخرى في الدقة والسرعة. ومع وجود نماذج مختلفة منها مثل الشبكات العصبية الالتفافية CNN والشبكات العصبية المتكررة RNN والمشفرات التلقائية Autoencoders والتعلم العميق Deep Learning وغيرها، أصبحت أهمية الشبكات العصبية لعلماء البيانات أو ممارسي التعلم الآلة مثل أهمية الانحدار الخطي للإحصائيين. لذلك من الضروري أن يكون لدينا فهم أساسي لماهية الشبكة العصبية وكيف تتكون وما هو مدى انتشارها وما هي حدودها. يحاول هذا المقال شرح الشبكة العصبية بدءً من لبناتها الأساسية وهي الخلايا العصبية وانتهاءً بأكثر أشكالها شيوعًا كالشبكات العصبية الالتفافية CNN والشبكات العصبية المتكررة RNNوغيرها.

ما هي الخلايا العصبية؟

كما يُشير الاسم فإن الشبكات العصبية مستوحاة من البُنية العصبية للدماغ البشري ولذلك فإن أهم عنصر فيه يسمى الخلايا العصبية. تشبه وظائفها الخلايا العصبية البشرية، أي أنها تأخذ المدخلات وتطرح المخرجات. من الناحية الرياضية البحتة تعتبر الخلية العصبية في عالم التعلم الآلي عنصرًا مسؤولًا عن وظيفة رياضية ودورها الوحيد هو توفير المخرجات من خلال تطبيق تلك الوظيفة الرياضية على المدخلات المقدمة.

الصورة من غوغل

تُعرف الدالة المستخدمة في الخلايا العصبية عمومًا بأنها دالة تنشيط. تمت تجربة خمسة دوال تنشيط رئيسية حتى الآن وهي دالة الخطوة (Step Function)، الدالة السينية (Sigmoid Function)، دالة الظل الزائدية (Tanh Function)، دالة الوحدة الخطية المصححة (ReLU Function) ودالة الوحدة الخطية المصححة المتسربة (Leaky ReLU Function). كل من هؤلاء مفصل أدناه.

دوال التنشيط

دالة الخطوة (Step Function)

يتم تعريف دالة الخطوة على أنها

الصورة من غوغل

عندما يكون الناتج 1 إذا كانت قيمة x أكبر من الصفر، ويكون الناتج 0 إذا كانت قيمة x أقل من الصفر. كما يمكن لنا أن نرى أن دالة الخطوة غير قابلة للاشتقاق عند الصفر. تستخدم الشبكة العصبية حاليًا في طريقة الانتشار الخلفي (back propagation method) مع خوارزمية أصل التدرج (gradient descent) لحساب أوزان (القيم التي تربط العقد العصبية متمثلة بقيمة W) الطبقات المختلفة. بما أن دالة الخطوة غير قابلة للتفاضل عند الصفر فإنها غير قادرة على إحراز تقدم بطريقة خوارزمية أصل التدرج وتفشل في مهمة تحديث الأوزان(القيم).

للتغلب على هذه المشكلة تم تقديم الدالة السينية (Sigmoid Function) بدلاً من دالة الخطوة(Step Function).

الدالة السينية Sigmoid Function

يتم تعريف الدالة السينية أو الدالة اللوجيستية رياضيًا على أنها

الصورة من غوغل

تميل قيمة الدالة إلى الصفر عندما تميل z أو المتغير المستقل إلى اللانهاية السالبة وتميل إلى 1 عندما تميل z إلى اللانهاية الموجبة. يجب أن يوضع في الاعتبار أن هذه الدالة تمثل تقريبًا لسلوك المتغير التابع وهي افتراضية. الآن السؤال الذي يطرح نفسه هو سبب استخدامنا للدالة السينية (Sigmoid Function) كأحد دوال التقريب. هناك بعض الأسباب البسيطة لذلك.

1. لأنها تلتقط النظام اللاخطي في البيانات. وإن كان ذلك في شكل تقريبي، إلا أن مفهوم اللاخطية ضروري للنمذجة الدقيقة.

2. تعتبر الدالة السينية (Sigmoid Function) قابلة للتفاضل خلال جكيع العمليات وبالتالي يمكن استخدامها مع خوارزمية أصل التدرج والانتشار الخلفي لحساب أوزان الطبقات المختلفة.

3. تعتمد فرضية المتغير الحر لاتباع الدالة السينية (Sigmoid Function) على التوزيع الغاوسي (Gaussian) للمتغير المستقل وهو توزيع عام نراه لكثير من الأحداث التي تحدث بشكل عشوائي وهو جيد للبدء.

ولكن الدالة السينية (Sigmoid Function) تعاني من مشكلة تلاشي التدرجات. كما يتضح من الصورة، تقوم الدالة السينية (Sigmoid Function) تكدس مدخلاتها في نطاق إخراج صغير جدًا [0،1] ولها تدرجات شديدة الانحدار. وبالتالي، لا تزال هناك مناطق كبيرة من مساحة الإدخال حيث تنتج أكبر التغييرات في المدخلات تغييرًا صغيرًا جدًا في المخرجات. يشار إلى هذا باسم "مشكلة تلاشي التدرج". تزداد هذه المشكلة مع زيادة عدد الطبقات (او المستويات) وبالتالي يركد تعلم الشبكة العصبية عند طبقة معينة.

دالة الظل الزائدية Tanh Function

دالة الظل الزائدية (z) (Tanh Function) هي نسخة معدلة من الدالة السينية (Sigmoid Function) ونطاق إخراجها هو [- 1،1] بدلاً من [0،1] في الدالة السينية (Tanh Function). [1]

الصورة من غوغل

السبب العام لاستخدام دالة الظل الزائدية (Tanh Function) في بعض الأماكن بدلاً من الدالة السينية (Sigmoid Function) هو أنه عندما تتمحور البيانات حول 0 فإن المشتقات تصبح أعلى. يساعد التدرج العالي في معدل تعلم أفضل. الصورة أدناه ترسم تدرجات دالة الظل الزائدية والدالة السينية. [2]

بالنسبة إلى دالة الظل الزائدية (Tanh Function)، فإن الإدخال بين [-1،1] ينتج لدينا مشتقًا بين [0.42، 1].

أما بالنسبة للدالة السينية (Sigmoid Function) ، فإذا كان الادخال بين [0،1] فإن المشتق يكون بين [0.20 ، 0.25]

الصورة من غوغل

كما نرى في الصور أعلاه فإن دالة الظل الزائدية (Tanh Function) لديها نطاق مشتق أعلى من الدالة السينية (Sigmoid Function) وبالتالي لديها معدل تعلم أفضل. ومع ذلك فإن مشكلة تلاشي التدرجات لا تزال قائمة في دالة الظل الزائدية (Tanh Function).

دالة الوحدة الخطية المصححة ReLU Function

دالة الوحدة الخطية المصححة (ReLU Function) هي دالة التنشيط الأكثر استخدامًا في نماذج التعلم العميق. تمنح الدالة 0 إذا تلقت أي إدخال سالب ولكن تلقت أية قيمة موجبة x فإنها تمنح تلك القيمة مرة أخرى. لذلك يمكن كتابتها كـما يلي: f(x)=max (0, x)

من الناحية التخطيطية تبدو هذه الدالة هكذا [3]

الصورة من غوغل

دالة الوحدة الخطية المصححة المتسربة Leaky ReLU Function

تعتبر دالة الوحدة الخطية المصححة المتسربة (Leaky ReLU Function) من أكثر الدوال شهرة. كما انها تعمل بنفس طريقة دالة الوحدة الخطية المصححة (ReLU Function) للأرقام الموجبة ولكن بدلاً من أن تكون 0 لجميع القيم السالبة يكون لها ميل ثابت (أقل من 1.).

هذا المنحنى هو عنصر يحدده المستخدم عند بناء النموذج وغالبًا ما يطلق عليه اسم α (ألفا). على سبيل المثال، إذا قام المستخدم بتعيين α = 0.3 فإن دالة التنشيط هي f(x) = max (0.3*x, x) x) له ميزة نظرية وهي أنه من خلال التأثر بـ x في جميع القيم فإنه قد يؤدي إلى المزيد من الاستخدام الكامل للمعلومات الواردة في x.

هناك بدائل أخرى ولكن الممارسين والباحثين بشكل عام لم يجدوا فائدة كافية لتبرير استخدام أي دالة اخرى بدلًا من دالة الوحدة الخطية المصححة (ReLU Function). في الممارسة العامة أيضًا ثبت أن دالة الوحدة الخطية المصححة (ReLU Function) تعمل بشكل أفضل من الدوال السينية (Sigmoid Function) ودالة الظل الزائد (Tanh Function).

الشبكات العصبية

قمنا فيما سبق بتغطية وظائف الخلايا العصبية ودوال التنشيط التي تشكل معًا اللبنات الأساسية لأي شبكة عصبية. وفيما يلي سوف نتعمق في دراسة الشبكة العصبية وأنواعها المختلفة. أود أن أقترح بشدة على الأشخاص إعادة النظر في الخلايا العصبية ودوال التنشيط إذا كان لديهم تشكيك في ذلك.

قبل فهم الشبكة العصبية، من الضروري فهم ماهية الطبقة (او المستوى) Layer في الشبكة العصبية. الطبقة ليست سوى مجموعة من الخلايا العصبية التي تأخذ المدخلات وتطرح المخرجات. تتم معالجة المدخلات لكل من هذه الخلايا العصبية من خلال دوال التنشيط المخصصة للخلايا العصبية. إليك مثالًا عن شبكة عصبية صغيرة.

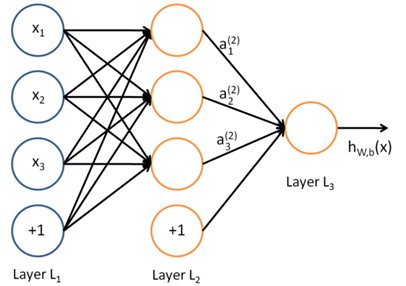
الصورة من غوغل

تسمى الطبقة الموجودة في أقصى اليسار "طبقة الإدخال" وتسمى الطبقة الموجودة في أقصى اليمين "طبقة الإخراج" (والتي تحتوي في هذا المثال على عقدة واحدة فقط). تسمى الطبقة الوسطى من العقد "الطبقة المخفية "لأنه لا يتم ملاحظة قيمها في مجموعة التدريب. نقول أيضًا أن مثالنا للشبكة العصبية به 3 وحدات إدخال (بدون حساب وحدة التحيز) و3 وحدات مخفية ووحدة إخراج واحدة [4]

تحتوي أي شبكة عصبية على طبقة إدخال واحدة وطبقة إخراج واحدة. اما عدد الطبقات المخفية فيختلف حسب اختلاف الشبكات اعتمادًا على مدى تعقيد المشكلة المراد حلها.

هناك نقطة مهمة أخرى يجب ملاحظتها هنا وهي أن كل طبقة من الطبقات المخفية يمكن أن يكون لها دالة تنشيط مختلفة، مثلًا، قد تستخدم الطبقة المخفية الأولى الدالة السينية (Sigmoid Function) وقد تستخدم الطبقة المخفية الثانية دالة الوحدة الخطية المصححة (ReLU Function) متبوعة بـدالة الظل الزائدية (Tanh Function) في الطبقة المخفية الثالثة كلها في نفس الشبكة العصبية. يعتمد اختيار ذالة التنشيط التي سيتم استخدامها مرة أخرى على المشكلة المعنية ونوع البيانات المستخدمة.

الآن لكي تقوم الشبكة العصبية بعمل تنبؤات دقيقة، يتعلم كل من هذه الخلايا العصبية أوزانًا (w) معينة في كل طبقة. تسمى الخوارزمية التي يتعلمون من خلالها الأوزان بالانتشار الخلفي back) (propagation والتي لن نتعرض لها بالتفصيل في هذا المقال.

يشار إلى الشبكة العصبية التي تحتوي على أكثر من طبقة مخفية باسم الشبكة العصبية العميقة Deep Neural Network.

الشبكات العصبية الالتفافية (CNN)

الشبكات العصبية الالتفافية (CNN) هي إحدى الأشكال المختلفة للشبكات العصبية المستخدمة بكثرة في مجال رؤية الكمبيوتر وتستمد اسمها من نوع الطبقات المخفية التي تتكون منها. تتكون الطبقات المخفية للشبكة العصبية الالتفافية CNN عادةً من طبقات التفافية (convolutional layers) وطبقات تجميع (pooling layers) وطبقات متصلة بالكامل (fully connected layers) وطبقات تسوية (normalization layers). هذا يعني ببساطة أنه بدلاً من استخدام دوال التنشيط العادية المحددة أعلاه يتم استخدام دوال الالتفاف والتجميع كدوال تنشيط.

لفهم الشبكات العصبية الالتفافية CNN بالتفصيل يجب أن نفهم معنى الالتفاف والتجميع. تم استعارة كلا المفهومين من مجال رؤية الكمبيوتر وتم تعريفهما أدناه.

الالتفاف: يعمل الالتفاف على إشارتين (في 1D) أو صورتين (في 2D): يمكنك التفكير في إحداهما على أنها إشارة "إدخال" (أو صورة) والأخرى (تسمى النواة) على أنها "مُرشِح (Filter)" على إدخال صورة مما ينتج صورة مخرجة (لذلك يأخذ الالتفاف صورتين كمدخلات وينتج صورة ثالثة كمخرج). [5]

بشكل عام، يأخذ الالتفاف إشارة الإدخال ويطبق فوقه مُرشِح (Filter)كما يضاعف بشكل أساسي إشارة الإدخال مع النواة للحصول على الإشارة المعدلة. رياضيا، يتم تعريف التفاف الدالتين f و g على أنهما

والتي ليست سوى حاصل الضرب النقطي لدالة الإدخال ودالة النواة.

في حالة التي تعالجها الصورة، يكون من الأسهل تصور النواة على أنها تنزلق فوق صورة كاملة وبالتالي تقوم بتغيير قيمة كل بكسل في العملية.

الصورة من غوغل

حقوق الصورة: آلة التعليم جورو Machine Learning Guru [6]

التجميع: التجميع هو عملية تقطيع تعتمد على عينة. الهدف هو اختزال عينة تمثيل الإدخال (صورة أو مصفوفة إخراج الطبقة المخفية أو غيرها) وتقليل أبعادها والسماح بوضع افتراضات حول الميزات الموجودة في المناطق الفرعية التي تم تجميعها.

هناك نوعان رئيسيان من التجميع وهما التجميع الأقصى والتجميع الأدنى. كما يوحي الاسم، يعتمد التجميع الأقصى على التقاط الحد الأقصى للقيمة من المنطقة المحددة ويستند التجميع الأدنى إلى اختيار الحد الأدنى للقيمة من المنطقة المحددة.

عنوان الصورة: وهكذا كما يمكن لنا أن نستنتج أن الشبكة العصبية الالتفافية CNN هي في الأساس شبكة عصبية عميقة تتكون من طبقات مخفية لها دوال الالتفاف والتجميع بالإضافة إلى دوال التنشيط لتقديم العناصر اللاخطية. يمكن العثور على شرح أكثر تفصيلاً في الموقع التالي: http://colah.github.io/posts/2014-07-Conv-Nets-Modular/ الشبكات العصبية المتكررة (RNN) الشبكات العصبية المتكررة RNN هي نوع مهم جدًا من الشبكات العصبية المستخدمة بكثافة في عملية "معالجة اللغة الطبيعية" (Natural Language Processing). في الشبكة العصبية العامة، تتم معالجة المدخلات من خلال عدد من الطبقات ثم يتم طرح المخرجات مع افتراض وجود مدخلين متتاليين مستقلان عن بعضهما البعض. إلا أن هذا الافتراض غير صحيح في عدد من سيناريوهات الحياة الواقعية. على سبيل المثال، إذا أراد أحدنا التنبؤ بسعر السهم في وقت معين أو التنبؤ بالكلمة التالية في سلسلة ما، فمن الضروري أن يؤخذ في الاعتبار الاعتماد على الملاحظات السابقة. تسمى هذه الشبكات متكررة لأنها تؤدي نفس المهمة لكل عنصر من عناصر التسلسل، مع اعتماد الإخراج على الحسابات السابقة. طريقة أخرى للتفكير في الشبكات العصبية المتكررة هي أن لديها "ذاكرة" تلتقط معلومات حول ما تم حسابه حتى الآن. من الناحية النظرية، يمكن لهذا النوع من الشبكات الاستفادة من المعلومات في تسلسلات طويلة بشكل اعتباطي وتعسفي، ولكنها في الممارسة تقتصر على النظر إلى الوراء بضع خطوات فقط. [7] من الناحية الهندسية -وكما يوضح الشكل أدناه كيف تبدو الشبكات العصبية المتكررة- يمكن لنا أن نتخيلها على أنها شبكة عصبية متعددة الطبقات حيث تمثل كل طبقة الملاحظات في وقت معين.

الصورة من غوغل

لقد أثبتت الشبكات العصبية المتكررة RNN نجاحها بشكل كبير في عملية معالجة اللغة الطبيعية خاصة مع متغيرها شبكة الذاكرة طويلة قصيرة المدى LSTM والتي يمكنها النظر إلى الوراء لفترة أطول من الشبكات العصبية المتكررة RNN. إذا كنت مهتمًا بفهم شبكة الذاكرة طويلة قصيرة المدى LSTM فعليك زيارة الموقع التالي

حاولنا في هذا المقال تغطية الشبكات العصبية من الجانب النظري، بدءًا من البنية الأساسية والخلايا العصبية مرورًا بأكثر الشبكات العصبية انتشارًا. كان الهدف من هذه المقال جعل القراء يفهمون كيف تُبنى الشبكة العصبية من الصفر وما هي جميع المجالات التي تستخدمها وأكثر أشكالها نجاحًا.

من المعلوم أن هناك العديد من الأنواع الشائعة الأخرى التي سنحاول تناولها في المقالات اللاحقة. لا تتردد في اقتراح موضوع تريدنا أن نتناوله لاحقًا.

---

مراجع:

1. http://ufldl.stanford.edu/wiki/index.php/Neural_Networks

2. https://stats.stackexchange.com/questions/101560/tanh-activation-function-vs-sigmoid-activation-function

3. https://www.kaggle.com/dansbecker/rectified-linear-units-relu-in-deep-learning

4. http://ufldl.stanford.edu/tutorial/supervised/MultiLayerNeuralNetworks/

5. https://www.cs.cornell.edu/courses/cs1114/2013sp/sections/S06_convolution.pdf

6. http://machinelearninguru.com/computer_vision/basics/convolution/image_convolution_1.html

7. http://www.wildml.com/2015/09/recurrent-neural-networks-tutorial-part-1-introduction-to-rnns/

---

ترجمة:

عبدالكريم السيد

مراجعة و تدقيق:

زهراء الحمري

"خريجة علم حاسوب، مهتمة بالأبحاث العلمية والعمل التطوعي."