شرح فرضية ريمان "Riemann hypothesis"
- BHRRES

- Jan 31, 2021
- 20 min read
Updated: Apr 2, 2021

تتذكر الأعداد الأولية، أليس كذلك؟ تلك الأرقام التي لا يمكنك تقسيمها إلى أرقام أخرى إلا عندما تقسمها على نفسها أو على 1 صحيح .
هناك سؤال عمره 3000 عام ،وهو:
.p , 29 , 23 , 19 , 17 , 13 , 11 , 7 , 5 , 3 , 2 , 1
ما هو p ؟ 31 ، ما هو العدد التالي؟ إنه 37 ، ما بعد ذلك؟ 41، وبعد ذلك؟ 43. كيف ، ولكن ... كيف تعرف ما سيأتي بعد ذلك؟
قدم حجة أو صيغة تتنبأ (حتى بالكاد) بما سيكون عليه العدد الأولي التالي (في أي تسلسل أرقام معين)، وسوف يرتبط اسمك إلى الأبد بواحد من أعظم إنجازات العقل البشري، أمثال نيوتن وأينشتاين وجوديل، اكتشف لماذا تعمل الأعداد الأولية كما تفعل، ولن تضطر أبدًا إلى فعل أي شيء آخر مرة أخرى.
المقدمة
تمت دراسة خصائص الأعداد الأولية من قبل العديد من عمالقة الرياضيات في التاريخ، من أول اثبات على ما لا نهاية الأعداد الأولية بواسطة إقليدس، إلى الصيغة التي انتجها أويلر التي ربطت الأعداد الأولية بدالة زيتا، و من صياغة غاوس و ليجاندر لنظرية الأعداد الأولية إلى إثباتها بواسطة هادامار و دي لا فاليه بوسان، و لا يزال برنارد ريمان يسود عالم الرياضيات الذي حقق أكبر انجاز منفرد في نظرية الأعداد الأولية، كما ان أعماله التي وردت جميعها في ورقة مكونة من
8 صفحات نُشرت عام 1859 ، و أدت إلى اكتشافات جديدة وغير معروفة سابقًا حول توزيع الأعداد الأولية، وتعتبر حتى يومنا هذا واحدة من أهم الأوراق في نظرية الأعداد. منذ ان نشرت اوراقه، كانت ورقة ريمان هي المحور الرئيسي لنظرية الأعداد الأولية وكانت بالفعل السبب الرئيسي لإثبات شيء يسمى نظرية الأعداد الأولية في عام 1896 ، ومنذ ذلك الحين تم العثور على العديد من البراهين الجديدة، بما في ذلك البراهين الأولية من قبل سيلبرغ و إيردوس، ومع ذلك فإن فرضية ريمان حول جذور وظيفة زيتا لا تزال غامضة.
كم عدد الاعداد الأولية؟
لنبدأ بالسهل، نعلم جميعًا أن الرقم إما ان يكون أوليا أو مركبا وتتكون جميع الأرقام المركبة من اتحاد اعداد، كما يمكن تقسيمها (تحليلها إلى عوامل) إلى الناتج (أ × ب) من الأعداد الأولية. الأعداد الأولية بهذه الطريقة هي "لبنات بناء" أو "عناصر أساسية" للأرقام، لقد ثبت أن عددهم لا نهائي من قبل إقليدس أي 300 سنة قبل الميلاد، ويظهر برهانه الذكي ببساطة على النحو التالي:
نظرية إقليدس
افترض أن مجموعة من الأعداد الأولية ليست لانهائية ، قم بعمل قائمة بجميع الأعداد الأولية التي اخترتها ، بعد ذلك ، دع P يكون حاصل ضرب كل الأعداد الأولية في القائمة (اضرب كل الأعداد الأولية في القائمة) ، أضف 1 إلى الرقم الناتج ، Q = P +1 ، كما هو الحال مع جميع الأرقام يجب أن يكون هذا الرقم Q إما أوليًا أو مركبًا:
إذا كان Q عددًا أوليًا، فقد وجدت عددًا أوليًا لم يكن موجودًا في "قائمة جميع الأعداد الأولية".
إذا لم يكن Q عددًا أوليًا، فهو مركب، أي مكون من أعداد أولية، أحدها p، و يقسم Q (نظرًا لأن جميع الأرقام المركبة هي نتاج أعداد أولية). من الواضح أن كل عدد أولي p يشكل P يقسم P. إذا قسمت p كلاهما على P و Q ، فسيتعين أيضًا قسمة الفرق بين الاثنين ، وهو 1. لا يوجد عدد أولي يقسم 1 ، وبالتالي لا يمكن أن يكون الرقم p في قائمتك ، وهو تناقض آخر يتمثل في أن قائمتك تحتوي على جميع الأعداد الأولية.
سيكون هناك دائمًا عدد أولي آخر p غير موجود في القائمة والذي يقسم Q ، لذلك يجب أن يكون هناك عدد لا نهائي من الأرقام الأولية.
لماذا يصعب فهم الأعداد الأولية؟
مجرد حقيقة أن أي مبتدئ يفهم المشكلة التي أشرت إليها أعلاه، تتحدث عن مدى صعوبة ذلك. حتى الخصائص الحسابية للأعداد الأولية، رغم دراستها بشكل مكثف، لا تزال غير مفهومة جيدًا. المجتمع العلمي واثق جدًا من افتقارنا لقدرتنا على فهم كيفية تصرف الأعداد الأولية إلى حد أن تحليل الأعداد الكبيرة إلى عوامل (معرفة أي اثنين من الأعداد الأولية يضربان معًا لتكوين رقم) هو أحد أسس نظرية التشفير، إليك طريقة واحدة للنظر إليه:
نحن نفهم الأرقام المركبة جيدًا انها تلك الاعداد الغير الأولية والمكونة من أعداد أولية، ولكن يمكنك بسهولة كتابة صيغة تتنبأ و / أو تنشأ مركبات، وتسمى الصيغة المستخدمة للمركبات أي "المرشح المركب" بالغربال. المثال الأكثر شهرة هو "غربال إراتوستينس" من ج. 200 قبل الميلاد، ووظيفته ببساطة هي تحديد مضاعفات كل رئيس حتى حد معين، إذن خذ العدد الأولي 2 وحدد 4 ، 6 ، 8 ، 10 وهكذا ، بعد ذلك خذ 3 وحدد 6،9،12،15 وهكذا ، و ما سوف يتبقى لك هو الأعداد الأولية فقط ، على الرغم من سهولة فهمه ، إلا أن غربال إراتوستينس كما يمكنك أن تتخيله ، ليس فعالًا للغاية.
هناك دالة واحدة تبسط عملك بشكل كبير و هي n6 +/-1 ، هذه الدالة البسيطة تنتج جميع الأعداد الأولية باستثناء 2 و 3 ، وتزيل كل مضاعفات 3 وجميع الأرقام الزوجية. ضع لـ n = 1،2،3،4،5،6،7 وراجع النتيجة: 5،7،11،13،17،19،23،25،29،31،35،37،41،43 ، الأعداد الوحيدة غير الأولية الناتجة عن الدالة هي 25 و 35 ، والتي يمكن تحليلها إلى 5 × 5 و 5 × 7 على التوالي ، الأعداد الغير أولية التالية كما يمكنك أن تتخيل هي 49 = 7 × 7 ، 55 = 5 × 11 وهكذا ، بسيط أليس كذلك؟
لتوضيح ذلك بصريًا، استخدمت شيئًا أسميه "السلالم المركبة"، وهي طريقة بسيطة لمعرفة كيفية وضع الأرقام المركبة التي تم إنشاؤها بواسطة الدالة لكل عدد أولي ودمجها، في الأعمدة الثلاثة الأولى من الصورة أدناه، ترى بدقة الأرقام الأولية 5 و7 و11 مع كل سلم مركب ذي صلة يصل إلى 91، الفوضى في العمود الرابع والتي تُظهر كيف أزال الغربال جميع الأعداد باستثناء الأعداد الأولية، هي توضيح جيد لسبب صعوبة فهم الأعداد الأولية.

السلاسل المركبة
الموارد الأساسية ...
إذن ما علاقة كل هذا بهذا الشيء الذي ربما سمعت عنه والذي يسمى "فرضية ريمان"؟ حسنًا، لنقل ببساطة انه من أجل فهم المزيد عن الأعداد الأولية، توقف علماء الرياضيات في القرن التاسع عشر عن محاولة التنبؤ بيقين مطلق بمكان وجود العدد الأولي، وبدلاً من ذلك بدأوا في النظر إلى ظاهرة الأعداد الأولية ككل، هذا النهج التحليلي هو ما كان ريمان بارعًا فيه، وهو ما صنع فرضيته الشهيرة، قبل أن أشرح ذلك، من الضروري التعرف على بعض الموارد الأساسية وهي:
متسلسلة الهارمونيك (المتسلسلة المتناسقة)
المتسلسلة المتناسقة هي متسلسلة لا نهائية من الأرقام التي درسها نيكول أو رسمها لأول مرة في القرن الرابع عشر، يتعلق اسمها بمفهوم التوافقيات في الموسيقى، وهي إيحاءات أعلى من التردد الأساسي للنغمة، وتظهر المتسلسلة على النحو التالي:
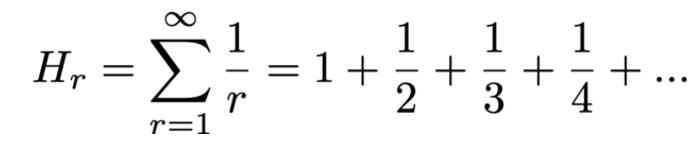
الحدود الأولية من المتسلسلة المتناسقة اللانهائية
وقد ثبت أن هذا المجموع متباعد من قبل أورسمه (ليس له حد محدود، ولا يقترب / يميل نحو أي رقم معين، ولكن ينطلق إلى اللانهاية).
دوال الزيتا
المتسلسلة المتناسقة هي حالة خاصة لنوع أكثر عمومية من الوظائف تسمى دالة زيتا (ζ (s ، يتم إعطاء دالة زيتا الحقيقية القيمة لـ r و n ، وهما رقمان حقيقيان:

دالة زيتا
إذا أدخلت قيمة n = 1 ، فستحصل على المتسلسلة المتناسقة التي تتباعد ،اما بالنسبة لجميع قيم n> 1 فإن المتسلسلة تتقارب ، مما يعني أن المجموع يميل نحو بعض الأرقام مع زيادة قيمة r ، أي أنه لا ينفد إلى اللانهاية.
صيغة منتج أويلر
أول ارتباط بين دوال زيتا والأعداد الأولية تم إجراؤه بواسطة أويلر عندما أوضح أنه بالنسبة إلى nو p، رقمان طبيعيان (أعداد صحيحة أكبر من الصفر) حيث يكون pأولي:

صيغة منتج أويلر لرقمين n ، p حيث كلاهما أكبر من الصفر و p عدد أولي
ظهر هذا التعبير لأول مرة في ورقة بحثية في عام 1737 بعنوان Variae Observationes circa series infinitas))، وينص التعبير على أن مجموع دالة زيتا يساوي حاصل ضرب مقلوب واحد ناقص مقلوب الأعداد الأولية إلى القوة s، وضع هذا الارتباط المذهل الأساس لنظرية الأعداد الأولية الحديثة، والتي منذ هذه النقطة استخدمت دالة زيتا ζ (s) كطريقة لدراسة الأعداد الأولية، إثبات الصيغة هو أحد الأشياء المفضلة لدي، ولذا سأقوم بتضمينها على الرغم من أنها ليست ضرورية تمامًا لأغراضنا (إنها جميلة جدًا!):
إثبات صيغة منتج أويلر
يبدأ أويلر بوظيفة زيتا العامة:

دالة زيتا
أولاً، يضرب كلا الطرفين في الحد الثاني:

دالة زيتا مضروبة في 1/2 ^ s
ثم يطرح التعبير الناتج من دالة زيتا:

دالة زيتا ناقص 1/2 ^ s مضروبة في دالة زيتا
يكرر هذه العملية، بعد ذلك يضرب كلا الطرفين في الحد الثالث:

دالة زيتا ناقص 1/2 ^ s مضروبة في دالة زيتا 1/3 ^ s
ثم نطرح التعبير الناتج من دالة زيتا:

دالة زيتا ناقص 1/2 ^ s مضروبة في دالة زيتا ناقص 1/3 ^ s مضروبة في دالة زيتا
بتكرار هذه العملية إلى ما لا نهاية، سيترك المرء في النهاية مع التعبير:

1 ناقص جميع المقلوب الأولية، مضروبًا في دالة زيتا
إذا كانت هذه العملية مألوفة لك، فذلك لأن ما أنشأه أويلر كان في الواقع غربالًا يشبه إلى حد كبير غربال إراتوستينس، يقوم بتصفية الأعداد غير الأولية من دالة زيتا.
بعد ذلك، قسّم التعبير على جميع الحدود المتبادلة الأولية، واحصل على:

علاقة دالة زيتا مع الأعداد الأولية، للأعداد الأولية 2،3،5،7 و 11
باختصار، لقد أظهرنا أن:

صيغة منتج أويلر، التعريف الذي يظهر العلاقة بين الأعداد الأولية ودالة زيتا
ألم يتم ذلك بشكل جميل؟ ضع s = 1 ، وابحث عن المتسلسلة المتناسقة اللانهائية ، مع إعادة إثبات اللانهاية للأعداد الأولية.
دالة موبيوس
أعاد أوغست فيرديناند موبيوس في وقت لاحق كتابة صيغة منتج أويلر لإنشاء مجموع جديد، بالإضافة إلى احتوائها على معادلات الأعداد الأولية، تحتوي دالة موبيوس أيضًا على كل عدد طبيعي ناتج عن أعداد فردية وزوجية للعوامل الأولية، الأرقام المتبقية من سلسلته هي تلك التي تقسم على بعض المربعات الأولية، ان مجموعه المشار إليه بواسطة (μ (nهو كما يلي:

دالة موبيوس، نسخة معدلة من صيغة منتج أويلر، محددة لجميع الأعداد الطبيعية
يحتوي المجموع على معاملات مثل:
كل عدد اولي
كل رقم طبيعي ناتج عن عدد فردي من الأعداد الأولية المختلفة، مسبوقة بعلامة ناقص و...
كل رقم طبيعي ناتج عن عدد زوجي من الأعداد الأولية المختلفة، مسبوقة بعلامة الجمع ؛..
فيما يلي الحدود الأولى:
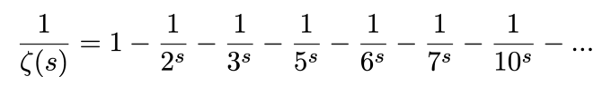
متسلسلة / مجموع لـ 1 مقسومًا على دالة زيتا (ζ (s
لا يحتوي المجموع على مقلوب الأعداد التي تقسم على بعض المربعات الأولية، على سبيل المثال 4، 8، 9 وهكذا، كما تأخذ دالة موبيوس μ (n) فقط ثلاث قيم محتملة والتي إما أن تكون بادئة (1 أو -1) أو تزيل حدود الـ (0) من المجموع:

القيم الثلاث الممكنة لدالة موبيوس(μ (n
على الرغم من ان موبيوسحددها رسميًا لأول مرة، إلا أن غاوس نظر في هذا المجموع الغريب بشكل ملحوظ في ملاحظة جانبية، قبل أكثر من 30 عامًا، عندما كتب:
"مجموع كل الجذور البدائية (للرقم الأولي p) إما ≡ 0 (عندما يكون p-1 قابلاً للقسمة على مربع)، أو ≡ ± 1 (mod p) (عندما يكون p-1 ناتجًا عن أعداد أولية غير متساوية) بحيث ان كان عدد هذه الإشارات موجبًا، ولكن إذا كان الرقم فرديًا، تكون الإشارة سالبة ".
الدالة المعدة للأعداد الأولية
لنعد إلى الأعداد الأولية، لفهم كيفية توزيع الأعداد الأولية أثناء صعودك إلى أعلى خط الأعداد دون معرفة مكان وجودها، من المفيد بدلاً من ذلك حساب عدد الأعداد حتى رقم معين.
دالة العد الاولي (π (x ، التي قدمها غاوس، تفعل ذلك بالضبط، وتعطي عدد الأعداد الأولية أقل من أو يساوي عددًا حقيقيًا معينًا، و نظرًا لعدم وجود صيغة معروفة لإيجاد الأعداد الأولية، فإن صيغة العد الأولي معروفة لنا فقط اما كرسم، أو زيادة دالة الخطوة بمقدار 1 عندما تكون x أولية، يظهر الرسم أدناه الدالة حتى x = 200.

دالة العد الأولي (π (x حتى x = 200
نظرية الأعداد الأولية

نظرية الأعداد الأولية
في اللغة الإنجليزية، تنص على ما يلي: "مع انتقال x إلى ما لا نهاية، فإن دالة العد الأولي (π (x ستقارب الدالة (x / ln (x”، أو بعبارة أخرى إذا عدت مرتفعًا بما يكفي، ورسمت عدد الأعداد الأولية حتى رقم كبير جدًا x، ثم رسمت xمقسومًا على اللوغاريتم الطبيعي لـ x، فستقترب النسبة بين الاثنين من 1 ، و قد تم رسم الدالتين أدناه بالنسبة إلى x = 1000:

دالة العد الأولي (π (x والتقدير من نظرية الأعداد الأولية المرسومة حتى x = 1000
من حيث الاحتمال، تنص نظرية الأعداد الأولية على أنه إذا اخترت عددًا طبيعيًا x عشوائيًا، فإن احتمال (P (x أن يكون هذا الرقم عددًا أوليًا هو حوالي 1 / (ln (x، هذا يعني أن متوسط الفجوة بين الأعداد الأولية المتتالية بين الأعداد الصحيحة الأولى x هو تقريبًا (ln (x.
دالة التكامل اللوغاريتمي
تُعرَّف الدالة (Li (x لجميع الأعداد الحقيقية الموجبة باستثناء x = 1. وهي مُعرَّفة بتكامل من 2 إلى x:

تمثيل التكامل لدالة التكامل اللوغاريتمي
برسم هذه الدالة جنبًا إلى جنب مع دالة العد الأولي والصيغة من نظرية الأعداد الأولية، نرى أن Li (x) هو في الواقع تقريب أفضل من (x / ln (x:

دالة التكامل اللوغاريتمي (Li (x ودالة العد الأولية (π (x و (x / ln (x مرسومة معًا
كم هو أفضل بكثير من التقريب! ويمكن رؤيته إذا قمنا بعمل جدول بقيم كبيرة لـ x، عدد الأعداد الأولية حتى x وخطأ الدوال القديمة (نظرية العدد الأولي) والدوال الجديدة (التكامل اللوغاريتمي):

عدد الأعداد الأولية حتى قوة معينة من عشرة وحدود الخطأ المقابلة للتقديرين
كما يمكن رؤيته بسهولة هنا، فإن دالة التكامل اللوغاريتمي أفضل بكثير من التقريب من الدالة من نظرية العدد الأولي، فقط "التجاوز" بمقدار 314890 عددا اوليا لـ x = 10إلى القوة 14، ومع ذلك تتقارب كلتا الدالتين نحو دالة العد الأولي π (س)، تعمل (Li (xأسرع بكثير، ولكن مع انتقال xإلى ما لا نهاية، فإن النسبة بين دالة العد الأولي وكلا
الدالتين (Li (xو (x / ln (xتتجه نحو 1. تصور:

تقارب نسب التقديرين ووظيفة العد الأولي نحو 1 مع x = 10000
دالة جاما
كانت دالة جاما (Γ (zموضوعًا مهمًا للدراسة منذ أن درس دانييل برنولي وكريستيان غولدباخ مشكلة توسيع دالة العامل إلى الحجج غير الصحيحة في عشرينيات القرن الثامن عشر. إنه امتداد لدالة مضروب (n! (1 x 2 x 3 x 4 x 5 x…. n ، إزاحة للأسفل بمقدار 1:
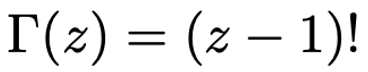
دالة جاما المحددة لـ z
تمثيلها بيانيا غريب للغاية:

دالة جاما (Γ (z المرسومة في النطاق -6 ≤ z ≤ 6
يتم تعريف دالة جاما (Γ (z لجميع القيم المركبة لـ z الأكبر من الصفر، الأعداد المركبة، كما تعلم على الأرجح، هي فئة من الأرقام ذات جزء تخيلي ، مكتوبة كـ (Re (z) + Im (z ، حيث (Re (z هو الجزء الحقيقي (العدد الحقيقي العادي) و (Im (z هو الجزء التخيلي، المشار إليه بالحرف i، عادةً ما يُكتب الرقم المركب بالصيغة +z = σ حيث يكون sigma σ هو الجزء الحقيقي وهو الجزء التخيلي، و تعتبر الأعداد المركبة مفيدة لأنها تسمح للرياضيين والمهندسين بتقييم المشكلات والعمل على حلها حيث لا تسمح الأعداد الحقيقية العادية بذلك.
تصور ان تعمل الأعداد المركبة على توسيع "خط الأرقام" التقليدي أحادي البعد إلى "مستوى" ثنائي الأبعاد ويسمى بالمستوى المركب، حيث يتم رسم الجزء الحقيقي من رقم مركب على المحور xويتم رسم الجزء التخيلي على المحور y.
لكي تكون قادرًا على استخدام دالة جاما (Γ (z ، تتم إعادة كتابتها في النموذج:

العلاقة الوظيفية لدالة جاما (Γ (z
باستخدام هذه التعريف، يمكن الحصول على قيم z تحت الصفر، ومع ذلك، فإنه لا يعطي قيمًا للأعداد الصحيحة السالبة، حيث لم يتم تعريفها (تقنيًا هي تفردات، أو أعمدة بسيطة).
زيتا وجاما
يتم توضيح الارتباط بين دالة زيتا ودالة جاما بالتكامل التالي:

برنارد ريمان
الآن بعد أن غطينا الموارد الأساسية الضرورية ، يمكننا أخيرًا البدء في الربط بين الأعداد الأولية وفرضية ريمان.
ولد عالم الرياضيات الألماني برنارد ريمان في مدينة بريسلينز عام 1826، نشر ريمان طالب غاوس أعمالًا في مجالات التحليل والهندسة و كانت أكبر مساهماته على الأرجح في مجال الهندسة التفاضلية ، حيث وضع الأساس للغة الهندسية المستخدمة لاحقًا في نظرية النسبية العامة لأينشتاين.

جهده الوحيد في نظرية الأعداد هو عبارة عن ورقته في كتابه المسمى (Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse) المنشورة عام 1859 بعنوان " حول عدد الأعداد الأولية الأصغر من عدد ما" أهم ورقة في هذا المجال. وأوضح في أربع صفحات قصيرة:
1 تعريف دالة زيتا لريمان ζ (s) ، دالة زيتا معقدة القيمة .
2 الاستمرار التحليلي لدالة زيتا لجميع الأعداد المركبة s ≠ 1.
3 تعريف لدالة ريمان xi ξ (s) ، دالة كاملة مرتبطة بدالة زيتا لريمان من خلال دالة جاما
4 إثباتان على المعادلة الوظيفية لدالة زيتا لريمان .
تعريف دالة العد الأولي لـ ريمان J (x) باستخدام دالة العد الأولي ودالة موبيوس .
صيغة واضحة لعدد من الأعداد الأولية الأقل من رقم معين باستخدام دالة العد الأولي لريمان ، المعرفة باستخدام الأصفار التي البسيطة زيتا لريمان .
إنه إنجاز مذهل للهندسة والإبداع ، ربما لم نشهد مثله منذ ذلك الحين ، هذا مذهل للغاية.
دالة زيتا لريمان
لقد رأينا العلاقة الخاصة بين الأعداد الأولية ودالة زيتا التي أظهرها أويلر في صيغة منتجه، بعيدًا عن هذا الارتباط ، لم يُعرف الكثير عن العلاقة وسيتطلب الأمر اختراع الأعداد المركبة لإظهار مدى الترابط بين الاثنين.

كان ريمان أول من نظر في دالة زيتا (ζ (s لمتغير معقد s ، حيث s = σ + it :
دالة زيتا لريمان لـ n ، حيث +s = σ هو رقم مركب ، و حيث كل من σ و t أرقام حقيقية
يُطلق عليها اسم دالة زيتا لريمان (ζ (s ، وهي متسلسلة لا نهائية تحليلية (لها قيم محددة) لجميع الأعداد المركبة ،مع جزء حقيقي أكبر من 1 (Re (s)> 1) ، و في هذا المجال ، تتقارب بشكل مطلق.

من أجل تحليل الدالة في مناطق خارج منطقة التقارب العادية (عندما يكون الجزء الحقيقي من المتغير المعقد أكبر من 1) ، يجب إعادة تعريف الدالة و قد نجح ريمان في القيام بذلك من خلال الاستمرار التحليلي لدالة متقاربة تمامًا في نصف المستوى Re (s)> 0.
الصيغة المعاد كتابتها لدالة زيتا لريمان ، حيث
x- | x = {x} |
هذا التعريف الجديد لدالة زيتا تحليلي في كل مكان في نصف المستوى Re (s)> 0 ، باستثناء s = 1 حيث يوجد قطب فردي / بسيط ،و يُطلق على هذه الدالة في هذا المجال مسمى الدالة جزئية الشكل ، لأنها متشابهة (معقد قابل للتفاضل في منطقة مجاورة لكل نقطة في مجالها) باستثناء القطب البسيط s = 1، وهي أيضًا مثال رائع لشيء يسمى متسلسلة دركليه اللامية .
لم يتوقف ريمان في ورقته عند هذا الحد ، و واصل تحليل دالة زيتا (ζ (s إلى المستوى المعقد بأكمله ، باستخدام دالة جاما (Γ (z، من أجل الحفاظ على بساطة هذه المقالة ، لن أعرض هذه الحسابات هنا ، لكنني أحثك بشدة على قراءتها بنفسك لأنها توضح حدس ريمان الرائع وتقنيته بشكل جيد للغاية (edit 03.13.20: the calculation is available in Veisdal (2013) pp. 28).

ستخدم ريمان في طريقته التمثيل المتكامل لجاما (Γ (z للمتغيرات المعقدة وشيء يسمى دالة ثيتا جاكوبي (ϑ (x ، والتي يمكن إعادة كتابتها معًا بحيث تظهر دالة زيتا.... حل لزيتا :
معادلة زيتا الوظيفية لكامل المستوى المعقد ماعدا فردين عند s = 0 و s = 1
في هذه الصورة ، يمكن للمرء أن يرى أن الحد (ψ (s يتناقص بسرعة أكبر من أي قوة x ، وبالتالي يتقارب التكامل مع جميع قيم s.
وللمضي قدمًا ، لاحظ ريمان أن الحد الأول في s(1 - s) /1- ثابت (لا يتغير) إذا استبدل أحد الأقواس بـ s 1 - ،كما انه عند القيام بذلك فإن ريمان يوسع من فائدة المعادلة عن طريق إزالة القطبين عند s = 0 و s = 1 ، وتحديد دالة ريمان (xi ξ (s بدون تفردات:
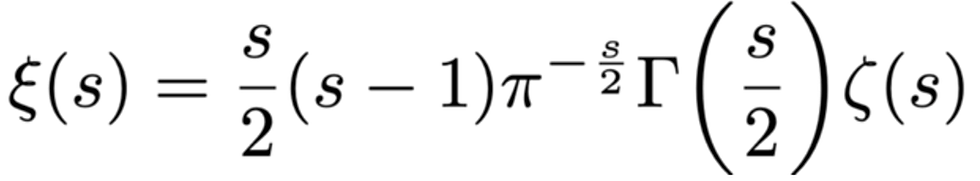
حلول معادلة زيتا لريمان
يمكن تقسيم جذور / أصفار دالة زيتا عندما تكون ζ (s) = 0 إلى نوعين تم تسميتهما بالأصفار " البسيطة" والأصفار " الغير بسيطة " لدالة زيتا لريمان.
وجود أصفار مع الجزء حقيقي Re (s) <0
الأصفار البسيطة هي الأصفار التي يسهل العثور عليها وشرحها ، و يمكن ملاحظتها بسهولة في الشكل الوظيفي التالي لدالة زيتا:
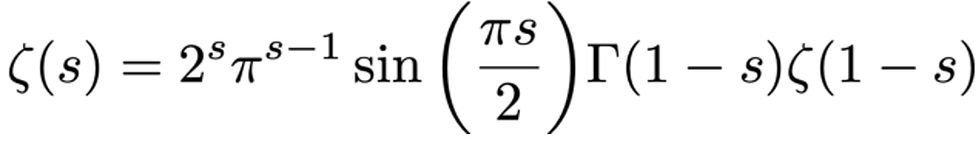
تباين في معادلة زيتا الوظيفية لريمان
صبح الناتج صفرًا عندما يصبح جزء الجيب صفرًا، انه يعمل كما تفعل kπ ، لذلك ، على سبيل المثال بالنسبة لعدد صحيح سالب زوجي s = -2n ، تصبح دالة زيتا صفرًا، و بالنسبة للأعداد الصحيحة الزوجية الموجبة s = 2n يتم إلغاء الأصفار بواسطة أقطاب دالة جاما (Γ (z ، من السهل رؤية هذا في الشكل الوظيفي الأصلي ، حيث إذا أدخلت s = 2n ، يصبح الجزء الأول من الحد غير محدد.

لذا ، فإن دالة زيتا ريمان لها أصفار في كل عدد صحيح سالب زوجي s = -2n ، هذه هي الأصفار البسيطة ، ويمكن رؤيتها في مخطط الدالة أدناه:

تم رسم دالة زيتا ريمان ζ (s) مع الأصفار البسيطة المميزة عند s = -2 ، -4 ، -6 وهكذا
وجود الأصفار مع الجزء الحقيقي Re (s)> 1
من صيغة منتج أويلر لزيتا ، يمكننا أن نرى على الفور أن زيتا (ζ (s لا يمكن أن تكون صفراً في المنطقة التي يكون الجزء الحقيقي من sأكبر من 1 ، لأن المنتج اللامتناهي المتقارب يمكن أن يكون صفراً فقط إذا كان أحد عوامله هو صفر، كما الدليل على اللانهاية من الأعداد الأولية ينفي هذا.

وجود الأصفار مع الجزء الحقيقي 0≤Re (s) ≤1
لقد وجدنا الآن أصفار زيتا البسيطة في نصف المستوى السالب عندما تكون Re (s) <0 ، وأظهرنا أنه لا يمكن أن يكون هناك أي أصفار في المنطقة Re (s)> 1، ومع ذلك ، فإن المنطقة الواقعة بين هذين المجالين ، والتي تسمى المقطع الحرج ، هي المكان الذي تم فيه الكثير من تركيز نظرية الأعداد التحليلية خلال مئات السنوات القليلة الماضية.

رسم الجزء الحقيقي والخيالي لوظيفة ريمان زيتا (ζ (s في الفاصل الزمني -5 <Re <2، 0 <Im <60
في الرسم أعلاه ، قمت برسم الأجزاء الحقيقية من زيتا (ζ (s باللون الأحمر والأجزاء التخيلية باللون الأزرق ، نرى أول صفرين بسيطين في أسفل اليسار عندما يكون الجزء الحقيقي من s هو -2 و -4. بين 0 و 1 ، قمت بتمييز المقطع الحرج وتمييزه حيث تتقاطع الأجزاء الحقيقية والخيالية من زيتا (ζ (s، و هذه هي الأصفار غير البسيطة لدالة زيتا لريمان. بالانتقال إلى القيم الأعلى ، نرى المزيد من الأصفار ، ودالتين تبدوان عشوائيتان ويبدو أنهما يزدادان كثافة مع زيادة الجزء التخيلي من s.

مخطط الأجزاء الحقيقية والخيالية لدالة زيتا لريمان (ζ (s في الفاصل الزمني -5 <Re <2 ، 0 <Im <120
دالة ريمان xi
لقد حددنا دالة ريمان(Xi ξ (s (نسخة المعادلة الوظيفية التي أزالت التفردات ، وبالتالي تم تعريفها لجميع قيم s) على النحو التالي:

دالة ريمان Xi (بدون تفردات)
هذه الدالة تستوفي العلاقة :

علاقة متناظرة بين القيم الموجبة والسالبة لدالة ريمان Xi
مما يعني أن الدالة متماثلة حول الخط العمودي Re (s) = 1/2 لذلكξ (1) ξ (0) = ، وξ (2) = ξ (-1) وهكذا، كما تُظهر هذه العلاقة الوظيفية) تناظر s و -s1 (جنبًا إلى جنب مع صيغة منتج أويلر أن دالة ريمانxi ξ (s) يمكن أن تحتوي فقط على أصفار في النطاق 0≤ Re (s) ≤ 1 أصفار ريمان بمعنى آخر ، وتتوافق دالة xi مع الأصفار غير البسيطة لدالة زيتا لريمان ، بمعنى ما ، الخط الحرج R (s) = 1/2 لدالة زيتا لريمان ζ (s) يتوافق مع الخط الحقيقي (Im (s) = 0) لدالة ريمان ξ (s) xi.
بالنظر إلى المخططين أعلاه ، يجب على المرء أن يلاحظ على الفور حقيقة أن جميع الأصفار غير البسيطة لدالة زيتا لريمان ζ (s) (أصفار دالة ريمان xi) لها جزء حقيقي Re (s) يساوي 1 / 2 ، علق ريمان بإيجاز على هذه الظاهرة في ورقته ، وهو تعليق عابر سينتهي به المطاف كواحد من أعظم موروثاته.
فرضية ريمان
الأصفار الغير بسيطة لدالة زيتا لريمان ζ (s) لها جزء حقيقي Re (s) = 1/2.
هذه هي الصيغة الحديثة للتخمين غير المثبت الذي قدمه ريمان في ورقته البحثية الشهيرة، بالكلمات تنص على أن النقاط التي تساوي فيها زيتا صفرًا ζ (s) = 0 في المقطع الحرج (1 ≤ 0≤ Re(s ، تحتوي جميعها على جزء حقيقي (Re (s = ½، و إذا كان هذا صحيحًا ، فإن جميع أصفار زيتا غير البسيطة ستكون على شكل (ζ (1/2 + ذلك و العبارة المكافئة لذلك (بيان ريمان الفعلي) هي أن جميع جذور دالة ريمان ξ (s) xi حقيقية.
في الرسم أدناه ، الخط Re (s) = 1/2 هو المحور الأفقي، و الجزء الحقيقي (Re (s من زيتا (ζ (s هو الرسم البياني الأحمر، والجزء التخيلي (Im (s هو الرسم البياني الأزرق. الأصفار غير البسيطة هي التقاطعات بين الرسم البياني باللونين الأحمر والأزرق على الخط الأفقي.

أول أصفار غير بسيطة لدالة زيتا لريمان على الخط Re (s) = 1/2.
إذا اتضح أن فرضية ريمان صحيحة ، فستظهر جميع الأصفار غير البسيطة للدالة على هذا الخط كتقاطعات بين الرسمين البيانيين.
أسباب تصديق الفرضية
هناك العديد من الأسباب لتصديق حقيقة فرضية ريمان حول أصفار دالة زيتا، و ربما يكون السبب الأكثر إقناعًا لعلماء الرياضيات هو العواقب التي قد تترتب على توزيع الأعداد الأولية ، يشير التحقق العددي من الفرضية إلى قيم عالية جدًا إلى حقيقتها، و في الواقع فإن الأدلة العددية للفرضية قوية بما يكفي لاعتبارها مثبتة تجريبياً في مجالات أخرى مثل الفيزياء والكيمياء، ومع ذلك فإن تاريخ الرياضيات يحتوي على العديد من التخمينات التي تم عرضها عدديًا لقيم عالية جدًا ولا تزال غير صحيحة.
يروي ديربيشاير (2004) قصة عدد سيكويز ، وهو رقم كبير جدًا أعطى حدًا أعلى ، مما يثبت زيف أحد تخمينات غاوس بأن التكامل اللوغاريتمي Li (x) دائمًا أكبر من دالة العد الأولي، و قد تم دحضها من قبل ليتلوود بدون مثال ، ثم يظهر أنه يجب أن يفشل فوق عدد سيكويز الكبير جدًا جدًا اي عشرة أس عشرة ، إلى قوة عشرة ، إلى قوة 34 ، مما يوضح أنه على الرغم من أن فكرة غاوس قد ثبت أنها خاطئة ، إلا أنه مثال على المكان الذي لا يمكن الوصول إليه في الحساب العددي حتى اليوم ، قد يكون هذا أيضًا هو الحال بالنسبة لفرضية ريمان ، التي تم التحقق منها "فقط" حتى عشرة أس اثني عشر أصفارًا غير بسيطة .
دالة زيتا لريمان والأرقام الأولية
باستخدام حقيقة فرضية ريمان كنقطة انطلاق ، بدأ ريمان بدراسة نتائج فرضيته، كتب في ورقته "... من المحتمل جدًا أن تكون كل الجذور حقيقية، بالطبع يرغب المرء هنا في دليل صارم ،و لدي في الوقت الحالي بعض من المحاولات اليائسة، و لكن مؤقتًا ضع البحث عن هذا جانبًا ، لأنه يبدو أنه يمكن الاستغناء عنه للهدف التالي من بحثي " ، كان هدفه التالي هو ربط أصفار دالة زيتا بالأعداد الأولية.
تذكر دالة العد الأولي (π (x التي تشير إلى عدد الأعداد الأولية التي تصل إلى عدد حقيقي يشمل x. استخدم ريمان (π (x لتحديد دالة العد الأولية الخاصة به ، وهي دالة العد الأولي لـ ريمان (J (x و يتم تعريفها على أنها :

دالة العد الأولي لريمان
أول شيء يجب ملاحظته حول هذه الدالة هو أنها ليست لانهائية ، في حد ما ستكون دالة العد صفراً لأنه لا توجد أعداد أولية لـ x <2، لذا بأخذ J (100) كمثال ، ستتكون الدالة من سبعة حدود لأن الحد الثامن سيتضمن ثمانية جذور من 100 ، وهو ما يساوي تقريبًا 1.778279 .. ، لذا فإن حد العد الأولي هذا يصبح صفرًا ويصبح المجموع J (100) = 28.5333….
و مثل دالة العد الأولي ، فإن دالة العد الأولي لـ ريمان J (x) هي دالة خطوة تزداد قيمتها عندما:

القيم المحتملة لدالة العد الأولي لريمان (j (x
لربط قيمة (J (x بعدد الأعداد الأولية التي تصل حتى إلى x ، نقوم باستعادة دالة العد الأولي (π (x من خلال عملية تسمى انعكاس موبيوس (والتي لن أعرضها هنا) ، و التعبير الناتج هو :

دالة العد الأولي (π (x وعلاقتها بدالة العد الأولي لريمان ، و دالة موبيوس (μ (n
تذكر أن القيم المحتملة لدالة موبيوس هي :

القيم الثلاث الممكنة لدالة موبيوس (μ (n
هذا يعني أنه يمكننا الآن كتابة دالة العد الأولي كدالة لدالة ريمان للعد الأولي ، مما يعطينا ذلك :

تم كتابة دالة العد الأولي كدالة ، لدالة العد الأولي لريمان للقيم السبع الأولى لـ n
لا يزال هذا التعبير الجديد مجموعًا محدودًا لأن J (x) تساوي صفرًا عندما تكون x <2 ، لأنه لا توجد أعداد أولية أقل من 2.
إذا نظرنا الآن إلى مثالنا عن J (100) ، فسنحصل على المجموع :

دالة العد الأولي لـ x = 100
الذي نعرف به عدد الأعداد الأولية أقل من 100.
ترجمة صيغة منتج اويلر
استخدم ريمان صيغة منتج أويلر كنقطة بداية واشتق طريقة للتقييم التحليلي للأعداد الأولية في لغة التفاضل والتكامل متناهية الصغر ، بدءًا من أويلر:

صيغة منتج أويلر للأعداد الأولية الخمسة الأولى
بأخذ لوغاريتم لكلا الجانبين أولاً ، ثم إعادة كتابة المقامات بين الأقواس ، فإنه يشتق العلاقة :

إعادة كتابة صيغة منتج أويلر باستخدام الوغاريتم
بعد ذلك ، باستخدام متسلسلة تايلور المعروفة ، قام بتوسيع كل حد لوغاريتمي على الجانب الأيمن ، مما أدى إلى إنشاء مجموع لا نهائي من المجاميع اللانهائية ، أي مجموع لكل حد في متسلسلة الأرقام الأولية.

متسلسلة تايلور للحدود الأربعة الأولى من لوغاريتم صيغة منتج أويلر
بالنظر إلى أحد هذه الحدود ، على سبيل المثال:

المصطلح الثاني في متسلسلة تايلور بمقدار 1/3 ^ s
يمثل هذا الحد، وكل حد آخر في الحساب ، جزءًا من المنطقة تحت دالة J (x)، مكتوبة كجزء لا يتجزأ:

شكل التكامل من الحد الثاني في متسلسلة تايلور 1/3 ^ s
بعبارة أخرى ، باستخدام صيغة منتج أويلر ، أوضح ريمان أنه من الممكن تمثيل دالة خطوة العد الأولية المنفصلة كمجموع مستمر للتكاملات، و يظهر الحد أدناه كمثال كجزء من المساحة تحت الرسم البياني لدالة العد الأولي لـ ريمان .

دالة العد الأولي لريمان (j (x حتى x = 50 ، مع تكاملين محددين في الرسم.
لذلك ، يمكن التعبير عن كل تعبير في المجموع المحدود الذي يشكل السلسلة المقلوبة الأولية لصيغة منتج أويلر في صورة تكاملات ، مما يجعله مجموعًا لا نهائيًا من التكاملات التي تتوافق مع المساحة الواقعة تحت دالة العد الأولي لـ Riemann، بالنسبة إلى العدد الأولي 3 يكون حاصل الضرب اللانهائي من التكاملات هو:

حاصل الضرب اللانهائي للتكاملات التي تشكل المنطقة تحت دالة العد الأولي التي يمثلها العدد الصحيح 3
بتجميع كل هذه المجاميع اللانهائية معًا في تكامل واحد ، يمكن كتابة التكامل تحت دالة العد الأولي لـ ريمان (J (x على النحو التالي:

لوغاريتم زيتا ، المعبر عنه بمتسلسلة لا نهائية من التكاملات
أو الشكل الأكثر شيوعًا :

التكافؤ الحديث لصيغة منتج أويلر ، الذي يربط دالة زيتا بدالة العد الأولي ريمان
ربط ريمان بهذا مع دالة زيتا (ζ (s ودالة العد الأولي الخاصة به ريمان (J (x في تعبير مكافئ بما يعادل صيغة منتج أويلر بلغة التفاضل والتكامل.
الحد الخطأ
بعد حصوله على نسخته التحليلية من صيغة منتج أويلر ، واصل ريمان بعد ذلك صياغة نظرية الأعداد الأولية الخاصة به، الشكل الصريح الذي قدمه هو:

"نظرية الأعداد الأولية لريمان" تخمين عدد الأعداد الأولية تحت مقدار معين x
هذه هي صيغة ريمان الدقيقة، إنه تحسين لنظرية الأعداد الأولية ، وهو تقدير أكثر دقة لعدد الأعداد الأولية الموجودة حتى و تضم العدد x ، و تحتوي الصيغة على أربعة حدود :
1- الحد لأول ، أو "الحد الأساسي" هو التكامل اللوغاريتمي (Li (x ، وهو أفضل تقدير لدالة العد الأولي (π (x من نظرية الأعداد الأولية، إنه إلى حد بعيد الحد الأكبر ، وكما رأينا سابقًا ، فهو مبالغة في تقدير عدد الأعداد الأولية حتى قيمة معينة x.
2- الحد الثاني ، أو "الحد الدوري" هو مجموع التكامل اللوغاريتمي لـ x أس ρ ، مُجمع على ρ ، وهي الأصفار غير البسيطة لدالة زيتا لريمان ، إنه الحد الذي يعدل المبالغة في تقدير الحد الأساسي.
3- والثالث هو ثابت -log (2) = -0.6993147 ...
4- الحد الرابع والأخير هو جزء لا يتجزأ من الصفر لـ x <2 ، لأنه لا توجد أعداد أولية أصغر من 2 ، وله قيمته القصوى عند 2 ، عندما يساوي تكامله تقريبًا 0.1400101….
الحدان الأخيران متناهيا الصغر في مساهمتهما في قيمة الدالة مع زيادة x، و العاملان الرئيسيان "المساهمان" بالنسبة للأعداد الكبيرة هما دالة التكامل اللوغاريتمي والمجموع الدوري. انظر إلى تأثيرها في الرسم البياني أدناه:

يتم تقريب دالة خطوة العد الأولية (π (x بالصيغة الدقيقة لدالة ريمان الأولية للعد (J (x باستخدام أول 35 صفراً غير بسيط ρ من دالة زيتا لريمان
في الرسم البياني أعلاه ، قمت بتقريب دالة العد الأولي (π (x باستخدام الصيغة الدقيقة لدالة ريمان الأولية للعد (J (x ، وتم تطبيقها على أول 35 صفراً غير بسيط لدالة زيتا لريمان (ζ (s ، و نرى أن الحد الدوري يتسبب في "صدى" الدالة والبدء في الاقتراب من شكل دالة العد الأولي (π (x.
أدناه يمكنك رؤية نفس الرسم البياني ، باستخدام المزيد من الأصفار غير البسيطة .

يتم تقريب دالة خطوة العد الأولية (π (x بالصيغة الدقيقة لدالة ريمان الأولية للعد (J (x باستخدام أول 100 أصفار غير بسيطة ρ من دالة زيتا لريمان .
باستخدام دالة ريمان الدقيقة ، يمكن للمرء تقريب عدد الأعداد الأولية بما يصل إلى رقم معين x وادراجها بدقة عالية جدًا. في الواقع ، أثبت فون كوخ في عام 1901 أن استخدام الأصفار غير البسيطة لدالة زيتا لريمان لتصحيح الخطأ لدالة التكامل اللوغاريتمي تعادل "أفضل حد ممكن" لحد الخطأ في نظرية الأعداد الأولية.
".. تعمل هذه الأصفار مثل أعمدة الهاتف ، والطبيعة الخاصة لوظيفة زيتا في ريمان تحدد بدقة كيف يجب ربط السلك - الرسم البياني - بينهما .." - دان روكمور
الخاتمة
منذ وفاة ريمان في عام 1866 عن عمر صغير يبلغ 39 عامًا ، ظلت ورقته البحثية الرائدة علامة بارزة في مجال نظرية الأعداد الأولية والتحليلية، و حتى يومنا هذا ، لا تزال فرضية ريمان حول الأصفار غير البسيطة لدالة زيتا لريمان دون حل ، على الرغم من البحث المكثف الذي أجراه العديد من علماء الرياضيات العظماء لمئات السنين، و يتم نشر العديد من النتائج والتخمينات الجديدة المرتبطة بالفرضية كل عام ، على أمل أن يكون الدليل في يوم من الأيام ملموسًا.
هذه المقالة هي نسخة مختصرة من رسالتي الجامعية "الأرقام الأولية و دالة زيتا لريمان ،الفرضية نفسها متاحة هنا ، و لأولئك المهتمين بمزيد من استكشاف الموضوع ، أوصي بشكل خاص بكتاب جون ديربيشاير "Prime Obsession".
المصدر:
The Riemann Hypothesis, explained | by Jørgen Veisdal | Cantor’s Paradise | Medium
ترجمة:
أروى الزقري
مراجعة وتدقيق:
صالح مهدي كاظم
"طالب رياضيات سنة ثالثة، مهتم بالرياضيات وبعض علوم اللغة العربية"




Comments